Hola, chicos
Envío Teoría y Práctica del MRU
Movimiento
rectilíneo uniforme (MRU)
El movimiento
rectilíneo uniforme (m.r.u.), es aquel con velocidad constante y cuya trayectoria es una línea recta. Un ejemplo claro son
las puertas correderas de un ascensor, generalmente se abren y cierran en línea
recta y siempre a la misma velocidad.
Observa que cuando
afirmamos que la
velocidad es constante estamos afirmando que no cambia ni su valor (también
conocido como módulo, rapidez o celeridad) ni
la dirección del movimiento.
Un movimiento
rectilíneo uniforme (m.r.u.) es aquel que tiene su velocidad
constante y su trayectoria es una línea recta. Esto implica que:
- El espacio
recorrido es
igual que el desplazamiento.
- En tiempos iguales se recorren distancias
iguales.
- La rapidez o
celeridad es
siempre constante y coincide con el módulo de la velocidad.
Ecuaciones y Gráficas del M.R.U.
Velocidad: En los m.r.u. la velocidad del cuerpo
es constante y por tanto igual a la velocidad inicial. Su unidad
en el Sistema Internacional (S.I.) es el metro por
segundo (m/s).
v=v0=cte
Dónde:
- v es la velocidad.
- v0 es la velocidad
inicial.
Posición:
Su unidad en el Sistema Internacional (S.I.) es
el metro (m) y se obtiene por medio de la siguiente expresión: x = x0 + v⋅t
Dónde:
- x0 es la posición
inicial.
- v es la velocidad que tiene el cuerpo a lo largo del movimiento.
- t es el intervalo de tiempo durante el cual se mueve el cuerpo.
Observa lo que t representa
en la ecuación de posición: El intervalo de tiempo durante el cual se
mueve el cuerpo. Dicho intervalo a veces es representado por t y
otras por ∆t.
En cualquiera de los casos, t=∆t
= tf – t - siendo tf y ti los instantes
de tiempo inicial y final respectivamente del movimiento que estamos
estudiando.
La
inclinación de la recta de la gráfica depende de la velocidad. A mayor
pendiente, mayor velocidad. Por otro lado, recuerda puedes deducir esta de la
gráfica de la fila superior teniendo en cuenta que la distancia recorrida
coincide con el área encerrada entre el eje x y la línea que representa la velocidad
en el intervalo de tiempo considerado (que en nuestro caso hemos llamado t).
PROBLEMAS DE ENCUENTRO:
Un problema típico en Física es el llamado problema de encuentro,
donde se trata de determinar la posición y el instante en que se
encuentran dos móviles de los cuales se conocen sus tipos de
movimientos.
Vamos a comenzar estudiando el encuentro entre dos móviles dotados de
M.R.U., de los cuales se conocen sus posiciones iniciales, velocidades e
instantes iniciales. Se determinará el instante en que se produce el encuentro
de dichos móviles y la posición en que ello ocurre.
En la siguiente aplicación interactiva se ilustra el problema del
encuentro de dos móviles con M.R.U.
Supongamos que un móvil “A” parte desde una posición XiA en
un instante tiA y con una velocidad constante vA.
Otro móvil “B” parte desde una posición XiB en
un instante tiB y con una velocidad constante vB.
Según la ecuación horaria del M.R.U. es:
Igualando ambas expresiones se obtiene una ecuación de primer grado en
“t”, la cual al resolverla arroja el valor del “tE”: tiempo
de encuentro de los móviles.
Es muy importante definir con precisión cual es el sistema de referencia
que se va a utilizar, a fin de colocar correctamente los valores de las
posiciones iniciales de ambos móviles, y considerar sus velocidades con el
signo que corresponda según que el móvil vaya en el sentido de crecimiento.
El encuentro se produce a las 13 horas y a 300 km del origen, como puede verse proyectando el punto de intersección de ambas rectas
sobre los
ejes coordenados.
TRABAJO PRÁCTICO 1: PROBLEMAS DE MRU
1) ¿A cuántos m/s equivale la velocidad de un móvil que se desplaza a 72
km/h?
2) Un móvil recorre 98 km en 1 hora
y 20 minutos, calcular:
a)
Su velocidad.
b)
b) ¿Cuántos kilómetros recorrerá en 3 h con
la misma velocidad?
3) Un móvil recorre una recta con velocidad constante. En los instantes t1
= 0 s y t2 = 4 s, sus posiciones son x1 = 9,5 cm y x2 = 25,5 cm. Determinar:
a)
Velocidad del móvil.
b) Su posición en t3 = 1 s.
c) Las ecuaciones de movimiento.
d) Su posición en el instante t4 =
2,5 s.
e) Gráfico v = f(t) del móvil.
f) Gráfico x = f(t) del móvil.
4) Se produce un disparo a 1,44 km de donde se encuentra un policía,
¿cuánto tarda el policía en oírlo si la velocidad del sonido en el aire es de 330
m/s?
5) ¿Cuánto tarda en llegar la luz del sol a la Tierra?, si la velocidad de
la luz es de 300.000 km/s y el sol se encuentra a 150.000.000 km de distancia.
6) ¿Cuál de los siguientes móviles se mueve con mayor velocidad: el (a)
que se desplaza a 120 km/h o el (b) que lo hace a 45 m/s?
7) ¿Cuál es el tiempo empleado por un móvil que se desplaza a 75 km/h para
recorrer una distancia de 25.000 m?
8) En una esquina, una persona ve como un muchacho pasa en su auto a una
velocidad de 20 m/s. Diez segundos después, una patrulla de la policía pasa por
la misma esquina persiguiéndolo a 30 m/s. Considerando que ambos mantienen su
velocidad constante, resolver gráfica y analíticamente:
a) ¿A qué distancia de la esquina, la policía
alcanzará al muchacho?
b) ¿En qué instante se produce el encuentro?
9) Un móvil sale de una localidad A
hacia B con una velocidad de 80
km/h, en el mismo instante sale de la localidad B hacia A otro a 60
km/h, A y B se encuentran a 600 km. Calcular:
a) ¿A qué distancia
de A se encontraran?
b) ¿En qué instante
se encontraran?
10) Un móvil sale de una localidad A
hacia B con una velocidad de 80
km/h, 90 minutos después sale desde el mismo lugar y en su persecución otro
móvil a 27,78 m/s. Calcular:
a) ¿A qué distancia de A lo alcanzará?
b) ¿En qué instante lo alcanzará?
11) Dos móviles pasan simultáneamente, con M.R.U., por dos posiciones A y B distantes entre si 3 km, con velocidades va = 54 km/h
y vb = 36 km/h, paralelas al segmento AB y del mismo sentido. Hallar analíticamente y gráficamente:
a) La posición del encuentro.
b) El instante del encuentro.
12) Dos móviles pasan simultáneamente, con M.R.U., por dos posiciones A y B distantes entre si 6 km, con velocidades va = 36 km/h
y vb = 72 km/h, paralelas al segmento AB y de sentido opuesto. Hallar analíticamente y gráficamente:
a) La posición del encuentro.
b) El instante del encuentro.




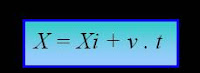



No hay comentarios:
Publicar un comentario